COMP7404 Computational Intelligence and Machine Learning
Topic 1 Solving Problems by Searching
Types of Search
- Uninformed Search (Know nothing about the problem except definition)
- Informed Search (know something more like how close to the goal)
- Local Search (Randomly initilize a state and make it better, e.g. Deep Learning)
- Constraint Satisfaction Problems (Know more about the problem)
- Adversarial Search (have an opponent, e.g. chess, star craft game)
Is Search the same as Unsupervised/Supervised Learning?
Search is a process that tries to explore all options and find out which one is best. Search itself isn’t considered as Machine Learning though it’s always combined with Machine Learning in some system to improve the performance. Machine Learning is part of Artificial Intelligence.
Search Applications
- Vacuum World
- Pancake Flipping
- 8 Puzzle
- Pathing
- TSP
- Game Play (chess, Go)
Any problem where more than one alternative needs to be explored may try search
Search Problem Definition
- States - Agent location, dirt location
- Initial State
- Actions and Transition Model
- available possible actions
- what each action does
- Goal Test
- Path Cost
A solution is a sequence of actions which transforms the start state to a goal state
State Space (the set of all reachable states)
- Usually a graph
- The possible action sequences form a search tree
State Space Graph vs. Search Tree
- State Space Graph (each state occurs only once)
- Nodes - states
- Arcs (connections between nodes) - action results
- A set of goal nodes - goal test
- Search Tree (states may occur more than once)
- Root - start state
- Nodes - possible action sequences
some related concepts:
- depth of tree
- branching factor (max children)
States vs. State Sequence
A large number of state space -> A huge number of state sequences (e.g. a large number of nodes in the search tree)
Example: Chess (10^43 possible states and 10^120 possible state sequences)
Romania Problem
- States
- The cities
- Initial State
- Arad
- Actions and Transition model
- Go to neighboring city
- Goal Test
- In Bucharest?
- Path Cost
- Distance between the cities
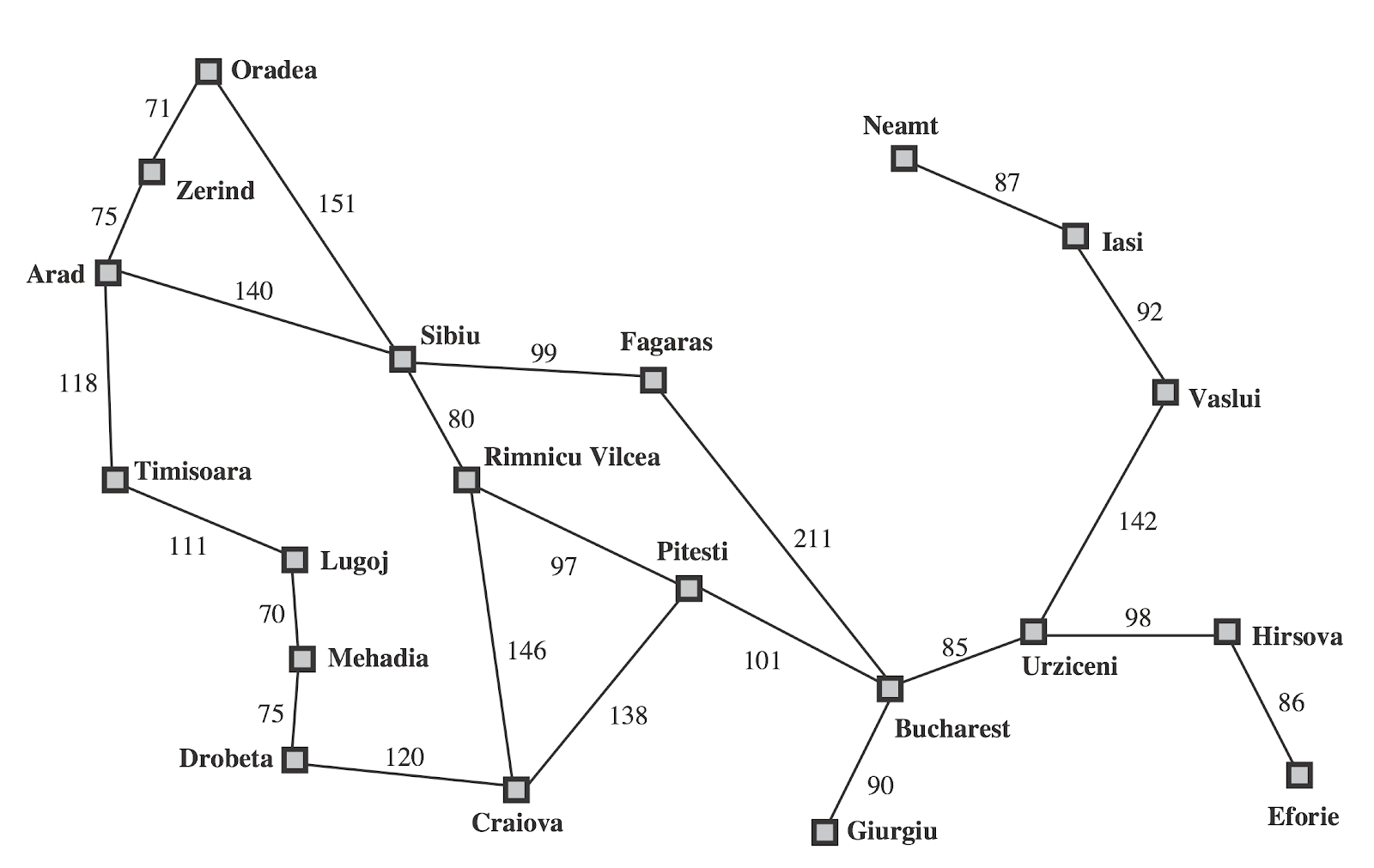
Store data in Python dictionary
romania = {
'A':['S','T','Z'],'Z':['A','O'],'O':['S','Z'],'T':['A','L'],'L':['M','T'],'M':['D','L'],
'D':['C','M'],'S':['A','F','O','R'],'R':['C','P','S'],'C':['D','P','R'],
'F':['B','S'],'P':['B','C','R'],'B':[]
}
Use dictionart to store neighbors for each cities
>>> romania['A']
['S', 'T', 'Z']
Search Strategy
- Defines the order of node expansion
- Evaluated along the following dimensions
- Completeness (always find a solution if exists)
- Optimality (find a least-cost solution)
- Time complexity (number of nodes generated)
- Space complexity (max number of nodes in memory)
Time/Space complexity
- b: maximum branching factor of the search tree
- d: distance to root of the shadowest solution
- m: maximum length of any path in the state space
Search Algorithms
Tree search algorithm(TSA)Graph search algorithm(GSA)
Uninformed (Blind) Search Strategies
- Breadth-first search (BFS)
- BFS-TSA
- BFS-GSA
- Depth-first search (DFS)
- DFS-TSA
- DFS-GSA
- Uniform-cost search (UCS)
- UCS-TSA
- UCS-GSA
BFS (Time and Space Complexity)
- Time - O(b^(d+1))
- Space - O(b^(d+1))
DFS (Space Complexity)
- Time - O(b^m)
- Space - O(m*b)
UCS (Time and Space Complexity)
- O(b^(C*/epsilon))
C*: cost of the optimal solution
epsilon: smallest path cost
Queue
class collections.deque([iterable[, maxlen]])
Returns a new deque object initialized left-to-right (using append()) with data from iterable.
If iterable is not specified, the new deque is empty.
>>> import collections
>>> queue = collections.deque(['A', 'B', 'C', 'D'])
>>> queue.popleft()
'A'
>>> queue
deque(['B', 'C', 'D'])
>>> queue.popleft()
'B'
>>> queue
deque(['C', 'D'])
TSA - BFS Version
When it applies DFS/UCS, only need to change the data type of the frontier variable.
pseudo code
function TSA(problem) returns solution
initialize frontier using initial state of problem
while frontier is not empty
choose a node and remove it from frontier
if node contains a goal state then return corresponding solution
explore the node, adding the resulting nodes to the frontier
actual python code
import collections
def bfsTsa(stateSpaceGraph, startState, goalState):
frontier = collections.deque([startState])
while frontier:
node = frontier.popleft()
if (node.endswith(goalState)): return node
for child in stateSpaceGraph[node[-1]]: frontier.append(node+child)
GSA - BFS Version
pseudo code
function GSA (problem) returns solution
initialize frontier using initial state of problem
initialize explored set to be empty
while frontier is not empty
choose a node and remove it from frontier
if node contains a goal state then return corresponding solution
If node is not in explored set
add node to explored set
explore the node, adding the resulting nodes to the frontier
actual python code
import collections
def bfsGsa(stateSpaceGraph, startState, goalState):
frontier = collections.deque([startState])
exploredSet = set()
while frontier:
node = frontier.popleft()
if (node.endswith(goalState)): return node
if node[-1] not in exploredSet:
exploredSet.add(node[-1])
for child in stateSpaceGraph[node[-1]]: frontier.append(node+child)
DFS
DFS explores the deepest node in the search tree
Stack
>>> import collections
>>> queue = collections.deque(['A', 'B', 'C', 'D'])
>>> queue.pop()
'D'
>>> queue
deque(['A', 'B', 'C'])
>>> queue.pop()
'C'
>>> queue
deque(['A', 'B'])
TSA - DFS Version
import collections
def dfsTsa(stateSpaceGraph, startState, goalState):
frontier = collections.deque([startState])
while frontier:
node = frontier.pop()
if (node.endswith(goalState)): return node
print('Exploring:',node[-1],'...')
for child in stateSpaceGraph[node[-1]]: frontier.append(node+child)
No results due to revisiting already explored nodes
GSA - DFS Version
import collections
def dfsGsa(stateSpaceGraph, startState, goalState):
frontier = collections.deque([startState])
exploredSet = set()
while frontier:
node = frontier.pop()
if (node.endswith(goalState)): return node
if node[-1] not in exploredSet:
exploredSet.add(node[-1])
for child in stateSpaceGraph[node[-1]]: frontier.append(node+child)
Choices of Search Algorithms
- BFS vs DFS
- Don’t use BFS when b (maximum branching factor) / d (distance to root of the shadowest solution) is big
- Don’t use DFS when m (maximum length of any path) is big
- Choose BFS is solution is close to the root of tree
- Choose DFS is solution is deep inside the search tree
- TSA vs GSA
- TSA (only frontier)
- Could stuck in infinite loops
- Explore redundant loops
- Require less memory
- Easier to implement
- GSA (froniter + explored set)
- Avoid infinite loops
- Eliminate many redundant paths
- TSA (only frontier)
Both have time complexity issue
UCS (Cheapest First Search)
Explores the cheapest node first
romania = {
'A':[(140,'S'),(118,'T'),(75,'Z')],'Z':[(75,'A'),(71,'O')],'O':[(151,'S'),(71,'Z')],
'T':[(118,'A'),(111,'L')],'L':[(70,'M'),(111,'T')],'M':[(75,'D'),(70,'L')], 'D':[(120,'C'),(75,'M')],'S':[(140,'A'),(99,'F'),(151,'O'),(80,'R')], 'R':[(146,'C'),(97,'P'),(80,'S')],'C':[(120,'D'),(138,'P'),(146,'R')], 'F':[(211,'B'),(99,'S')],'P':[(101,'B'),(138,'C'),(97,'R')],'B':[]}
Priority Queue in Python (Use heapq in Python3)
frontier = []
>>> from heapq import heappush, heappop
import random
>>> heappush(frontier, (random.randint(1, 10), 'A'))
>>> heappush(frontier, (random.randint(1, 10), 'B'))
>>> heappush(frontier, (random.randint(1, 10), 'C'))
>>> frontier
[(2, 'C'), (7, 'B'), (6, 'A')]
>>> heappop(frontier)
(2, 'C')
>>> heappop(frontier)
(6, 'A')
>>> heappop(frontier)
(7, 'B')
>>> (1, 'B') < (2, 'A')
True
>>> (1, 'B') < (1, 'A')
False
TSA - UCS Version
from heapq import heappush, heappop
def ucsTsa(stateSpaceGraph, startState, goalState):
frontier = []
heappush(frontier, (0, startState))
while frontier:
node = heappop(frontier)
if (node[1].endswith(goalState)): return node
for child in stateSpaceGraph[node[1][-1]]:
heappush(frontier, (node[0]+child[0], node[1]+child[1]))
GSA - UCS Version
from heapq import heappush, heappop
def ucsGsa(stateSpaceGraph, startState, goalState):
frontier = []
heappush(frontier, (0, startState))
exploredSet = set()
while frontier:
node = heappop(frontier)
if (node[1].endswith(goalState)): return node
if node[1][-1] not in exploredSet:
exploredSet.add(node[1][-1])
for child in stateSpaceGraph[node[1][-1]]:
heappush(frontier, (node[0]+child[0], node[1]+child[1]))
Informed Search
Employ problem specific knowledge beyond the definition of the problem itself
- Heuristic function
Example
- Greedy best-first search
- A* search
Heuristic Function (designed for a particular search problem)
A function that estimate how close you are to the goal
h(n)
- Cost of the cheapest path from the state at node n to a goal state
- If n is a goal node, h(n) = 0
Greedy Search (Best-first Search)
Expand the node that has the lowest h(n)
Updated Romania Problem Definition (Add h(n))
romaniaH = {
'A':366,'B':0,'C':160,'D':242,'E':161,'F':176,'G':77,'H':151,'I':226,
'L':244,'M':241,'N':234,'O':380,'P':100,'R':193,'S':253,'T':329,'U':80,
'V':199,'Z':374}
Greedy TSA Practice
from heapq import heappush, heappop
def greedyTsa(stateSpaceGraph, h, startState, goalState):
frontier = []
heappush(frontier, (h[startState], startState))
while frontier:
node = heappop(frontier)
if (node[1].endswith(goalState)): return node
for child in stateSpaceGraph[node[1][-1]]:
heappush(frontier, (h[child[1]], node[1]+child[1]))
A* Motivation UCS-TSA
orders by backward cost
g(n)
A* Motivation Greedy-TSA
orders by forward cost
h(n)
* always means optimal in AI
A* Motivation A*-TSA
orders by backward cost + forward cost
f(n) = g(n) + h(n)
A*-TSA Practice
from heapq import heappush, heappop
def aStarTsa(stateSpaceGraph, h, startState, goalState):
frontier = []
heappush(frontier, (h[startState], startState))
while frontier:
node = heappop(frontier)
if (node[1].endswith(goalState)): return node
for child in stateSpaceGraph[node[1][-1]]:
heappush(frontier, (node[0]+child[0]-h[node[1][-1]]+h[child[1]], node[1]+child[1]))
aStarMotivation = {
'S':[(1,'a')],'a':[(1,'b'),(3,'d'),(8,'e')],'b':[(1,'c')],'c':[],'d':[(2,'G')],'e':[(1,'d')]}
aStarMotivationH = {'S':6,'a':5,'b':6,'c':7,'d':2,'e':1,'G':0}
Admissibility of Heuristic
A heuristic h(n) is admissible (optimistic)
1 <= h(n) <= h(n)*
where h*(n) is the true cost of the nearest goal
Optimality of A*
A* is optimal if an admissible heuristic is used
Consistency of Heuristic
- Definition
- Heuristic cost <= actually cost for each arc
- h(a) - h(c) <= cost (a to c)
- Heuristic cost <= actually cost for each arc
- Consequence of consistency
- The f value along a path never decrease
- h(a) <= cost(a to c) + h(c)
- The f value along a path never decrease
